About a year ago I described the results of a preliminary project to scope out the possibility of making the InChI identifier play nice with inorganic & organometallic complexes. There’s now a followup increment that does likewise for some of the higher valence stereochemistry centres that are found in these complexes.

Most people who have dabbled with cheminformatics are familiar with the InChI identifier which is widely considered the best of breed way to “name” a structure by turning it into a canonical string, meaning that any two ways that a chemist may choose to draw a molecule results in the same identifier being produced. This characteristic is incredibly powerful because it can be used as a simple indexing system for databases, giving them the power of de-duplication with minimal effort.

One of the biggest shortcomings of InChI identifiers is shared with almost the entirety of the cheminformatics industry: it is only fit for purpose when applied to organic chemistry of the mainstream variety that is typically found in drug discovery projects. It is a product of its time, and suffers from the fact that the ubiquitous sketch format – MDL Molfile – had inherent limitations that made it impossible to represent most inorganic coordination complexes without making a heinous mess (e.g. implying the wrong molecular formula). Although these file format shortcomings have since been partially addressed, it is hard to tell how many of the reader/writer implementations have been updated. And even without file format problems, a bigger picture issue is the fact that the inorganic chemistry community has been largely excluded from participating in cheminformatics, and the common drawing conventions that are used in the literature create a number of disambiguation problems for machine readability (e.g. the use of a single line to denote covalent bonds and coordination bonds, even though they are completely different from a valence counting point of view).

The current InChI identifier takes a pragmatic approach to bonds between metals and their ligands: it simply deletes them. This is quite an egregious offence from the point of view of an inorganic chemist, but for purposes of disambiguation, it is actually quite reasonable: the frequency with which two inorganic compounds differ only by the way their ligand(s) are attached to the metal(s) is low, and so in principle it could be used as a pre-filter for which collisions happen quite rarely. Unfortunately this does not work very well, partially because of the aforementioned lack of good drawing practices for inorganic complexes, and because the InChI algorithm has quite a few standardisation rules that get applied to fragments before/after the disconnection, which are simply not appropriate for this use case. The bottom line is that it makes rather a mess, and so refitting the identifier to work with a large domain of chemistry requires either a major overhaul or an alternate strategy.

Part 1 of this study involved gathering a decent sized validation set containing ideally every known kind of inorganic bonding arrangement, drawn in a variety of ways ranging from ideal to awful-but-not-wrong (where not wrong is more or less defined as having the right molecular formula and having all bonding interactions included in the graph). The results are described in detail on the GitHub site for the project, and there are also slides from the San Diego 2019 meeting. A very rough summary of the work is that the algorithm looks for electron delocalisation islands and assumes that electrons and charges are free to travel within them, and builds a canonical representation accordingly. It sounds simple, and actually it sort of is: the single most important high level insight about doing cheminformatics with inorganic chemistry is that the number of rules that you can get away with having is perilously close to none at all – because inorganic chemists make their careers from breaking them, and they’ve gotten really good at it.

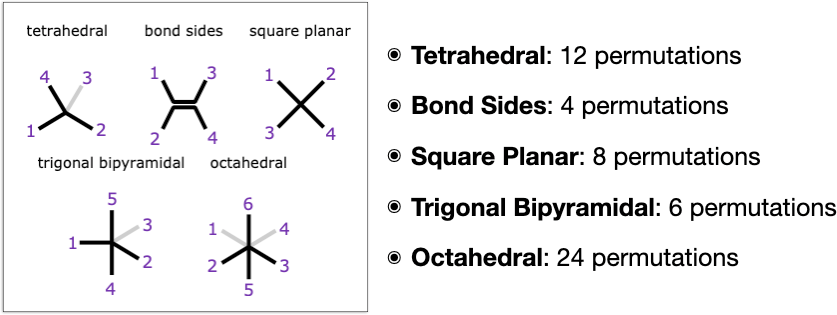
Part 2 of the study is based on following up the original work by adding in stereochemistry types that aren’t found in ordinary organic compounds, and these currently include 3 of the textbook classics: square planar, trigonal bipyramidal and octahedral. In addition to the baseline types of tetrahedral (R/S) and double bond (E/Z) that occur frequently in organic chemicals, this makes 5 types that are supported.

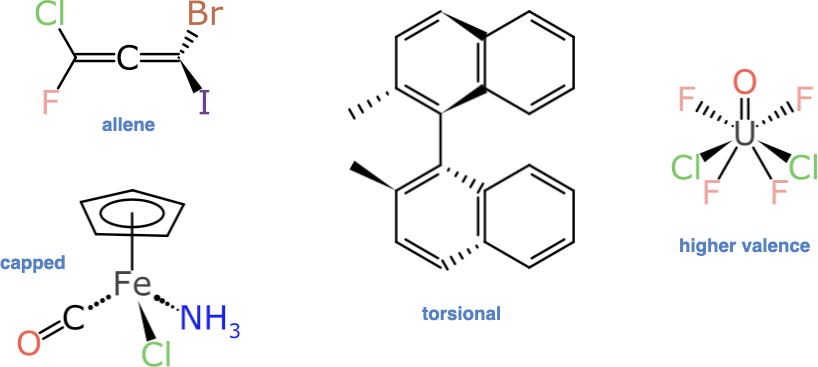
Anyone who has delved into the subject of stereochemistry will be well aware that there are quite a few ways to introduce “non-compositional asymmetry” to a molecule. These are some of the examples that have not been addressed:

Some of these are harder than others to identify and process, but fortunately the 4-, 5- and 6-coordinate atom-centred stereocentres make up most of the additional demand:

Even with just these extra types, there is quite a lot going on in the way of unexpected gotchas. First of all, each of these 5 types is unique in its own special way:

• Tetrahedral: from a stereochemistry point of view this is the highest symmetry type, because if you select any substituent, the other 3 substituents are all cis to it, which is not true for any of the other types. This is related to the fact that tetrahedral stereocentres have a meso plane of symmetry if any 2 substituents are identical, whereas if all substituents are different they make for enantiomers of which there are 2 possible types (which are different from diastereomers in that they are indistinguishable by most kinds of physical measurements). But of course these characteristics are not necessarily applicable when a stereocentre is fused into a ring and/or connected to other stereocentres: that always introduces the option of getting weird.
• Bond Sides: as the name suggests, this is the only type that is centred around a bond. Having a bond dividing the substituents into two sides introduces a constraint, and in fact this type of stereochemistry is very easy to encode as a special case. Algorithmically, though, it can be handled in a way that’s analogous to all the others by labelling both of the atoms that make up the stereo-bond and treating them independently.
• Square Planar: this is made up of 4 atoms in a plane, and is sort of what the bond-sides stereochemistry would be without the bond, or what tetrahedral stereochemistry would be if it were flattened onto a plane. Unlike tetrahedral, though, it does not give rise to enantiomers, only diastereomers (which is a property it shares with bond-sides). Square planar centres are stereochemically inactive if 3 or more substituents are the same. Perhaps annoyingly, if any 2 substituents are the same, there are only two possible isomers: cis and trans; but if all 4 substituents are different, there are 3 different possible configurations, which means it can’t be labelled with just one bit of information.
• Trigonal Bipyramidal: while not the most common geometry, it is abundant enough to require its own treatment. It is unique amongst all of these types in that the ligand positions are already asymmetric: there are 2 axial ligands and 3 equatorial, which means that there is stereochemical information if any of the 5 ligands is not the same as all the others. It is also permissible to have one of the axial positions vacant.
• Octahedral: the major distinction of this type is that it has the most substituents, and that octahedral centres often produce a variety of different possible enantiomer and diastereomer options at the same time. From the point of view of any selected ligand, there are 4 other ligands which are cis and one that is trans. Up two 2 spots can be vacant, though if they are opposite each other, it is just a form of square planar.

Implementation of the perception, representation and atom identity is described in a lot of detail in the README for the second half of the project, so I won’t go into specifics in this blog post. Suffice to say that building & passing the validation set involved a lot of expected challenges and quite a few more unexpected ones.

For the most part, dealing with these geometries is about as tricky as one would expect, for someone with a moderate amount of experience in coding up such things, if and only if there no pesky rings and the substituents distinguish themselves by compositional equivalence. By which I mean that in cases where ligands that are different have different atom & bond connectivity, and they’re not connected to each other, then it’s a pretty routine problem to solve. That’s the case for the bulk of stereo-active coordination complexes, and not so for a vast long tail that stretches out from here to infinity (or thereabouts).

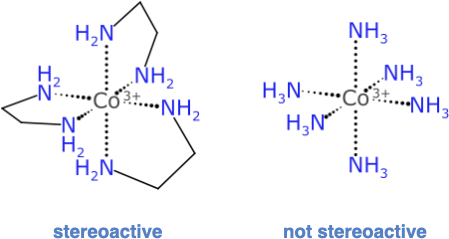
Consider this popular example that is used in teaching laboratories to extinguish hope for undergraduate chemists:

The complex on the left with 3 ethylenediamine ligands has an enantiomer: its mirror image is not superimposable; but the compositional equivalence of the 6 ligand attachment points suggests that it has the same ultra high symmetry as the complex on the right. But this is not so, because it matters which order these bidentate ligands are traversed in. For the hexammonium complex, though, picking any atom traversal order will give the same final result.

This barely even scratches the surface. Inorganic compounds just get bigger and weirder as the number of stereocentres and rings and rings-within-rings are dialled up: some of them aren’t as hard as they look, and work quite well once a general system has been designed:

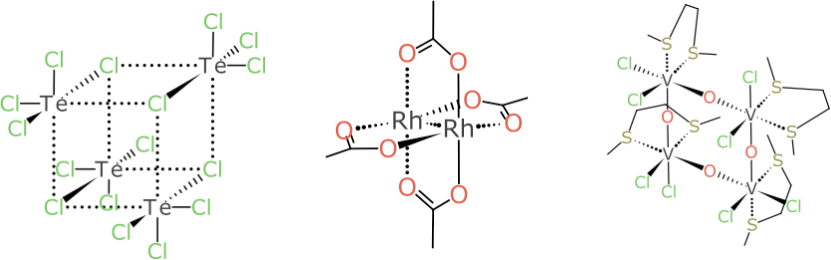
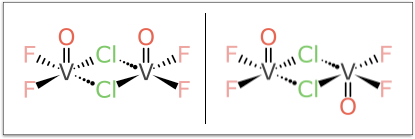
But the example that turned out to be the bane of my existence for multiple weekends is this pair:

It looks relatively harmless compared to some of the larger more foreboding cases, but don’t be fooled: try coming up with a rationalisation for designating the Vanadium atoms as (α,α) and (α,β) or vice versa, and do so without a kludgey rule, in such a way that it generalises to all kinds of related stereocentre combinations.

This is a sneak preview of some of the issues that keep life interesting, but there are a while lot more in the validation set that is part of the project: there are 158 stereochemistry examples, each of which has an equivalent & inequivalent partner, in order to test the same/different options. The non-stereo validation set is larger, and has 547 cases.

The whole project (both phases 1 & 2) has been heavily data driven from the very beginning, which is absolutely essential for a project like this. The validation sets are stacked almost entirely with real world examples, and perturbed in order to create adversarial cases to test the algorithm. All of this data gathering and wrangling was done by me, which is important, because in a past life I was a card-carrying inorganic chemist who worked with these compounds every day. Since leaving the bench, I’ve spent 20 years carrying around a chip on my shoulder, ruminating on the ways in which these complexes don’t work with most cheminformatics software.

This project has been funded by the InChI Trust organisation, which has aspired for some time now to extend the reach of the InChI technology to include a larger subset of chemistry. The so-called “coordination layer” is a proof of concept demonstration algorithm combined with the aforementioned validation sets, which exists for the primary purpose of demonstrating that InChI-type technology can be applied to coordination chemistry with efficacy that is quite comparable to that for the organic domain. Unfortunately the initial explorations in the first part demonstrated that it’s not really possible to just supplement the core InChI algorithm: instead either parts of it have to either be rearchitected (which brings some significant challenges) or it can be supplemented by creating an optional alternative layer (which has its own set of issues).

Nonetheless, the proof of concept algorithm is available now, if anyone wants to try it out. The easiest way is to try out the online demo, because clicking on a link is a bit easier than installing software. But there is a command line invocation, which allows you to feed in an SDfile and export an identifier for each molecule.